Çok eski bir web tarayıcısı kullanıyorsunuz. Bu veya diğer siteleri görüntülemekte sorunlar yaşayabilirsiniz..
Tarayıcınızı güncellemeli veya alternatif bir tarayıcı kullanmalısınız.
Tarayıcınızı güncellemeli veya alternatif bir tarayıcı kullanmalısınız.
Ömer Hayyam
- Konbuyu başlatan echo11
- Başlangıç tarihi
Benzer Konular
ÖMER HAYYÂM
عمر الخيّام
Ebü’l-Feth Gıyâsüddîn Ömer b. İbrâhîm el-Hayyâm (ö. 526/1132 [?])
İranlı âlim, şair ve filozof.
عمر الخيّام
Ebü’l-Feth Gıyâsüddîn Ömer b. İbrâhîm el-Hayyâm (ö. 526/1132 [?])
İranlı âlim, şair ve filozof.
430-439 (1039-1048) yılları arasında Horasan eyaletinin merkezi Nîşâbur’da doğdu. Öğrenimini ve hayatının büyük bir kısmını orada ve Semerkant’ta geçirdi. Sözlükte hayyâm kelimesi “çadır yapımcısı” anlamına gelmekle birlikte onun İran’da yerleşmiş Arap asıllı Hayyâmî kabilesine mensup olabileceği de düşünülmektedir. Kendisine büyük ilgi gösteren Selçuklu sultanlarının, Vezir Nizâmülmülk’ün saraylarında görev yapmaktan hoşlanmadı ve bilimsel araştırmalara adanmış sakin bir hayatı seçerek zaman zaman Semerkant, Buhara, Belh ve İsfahan gibi bilim ve sanat merkezlerinde dolaşmayı tercih etti. Semerkant’ta iken Ebû Tâhir isminde yüksek makam sahibi bir memurun himayesine girdi. Nîşâbur’da 517-526 (1123-1132) yılları arasında seksen beş yaşlarında öldüğü tahmin edilmektedir.

İbn Sînâ ekolüne mensup bir âlim-filozof olduğu kabul edilen Ömer Hayyâm cebir, geometri, astronomi, fizik ve tıpla ilgilenmiş, müzikle uğraşmış, ayrıca adını ölümsüzleştiren rubâîlerini kaleme almıştır. Ali b. Zeyd el-Beyhakī Hayyâm’ın hâfızasının fevkalâde kuvvetli olduğunu, dil, fıkıh, tarih ve kıraat sahalarında geniş mâlûmatı bulunduğunu, riyâziye, tıp ve diğer aklî ilimlerde eşsiz olduğunu söylerken Necmeddîn-i Dâye onun hakkında “bahtsız bir filozof, Allahsız ve maddeci” demektedir (İA, IX, 474). Ömer Hayyâm, Batı’da Doğu’nun en fazla hayranlık duyulan şairi ve en tanınmış âlimlerinden biridir. 1892’de Londra’da onun adına bir kulüp kurulmuş, 1970’te ayın üzerindeki bir kratere, 1980’de yeni bulunan bir kuyruklu yıldıza adı verilmiştir.

Hayyâm’ın genelde matematiğin ve özelde analitik geometrinin gelişimi üzerindeki etkisi çok büyüktür; çalışmaları Şerefeddin et-Tûsî’ye (ö. 610/1213 [?]) kadar İslâm matematiğinde, üçüncü dereceden denklemlerin çözümünde geometrik yaklaşımı benimseyen Descartes’a (ö. 1650) kadar Batı matematiğinde aşılamamıştır. Onun matematiğe ilişkin araştırmaları ve bilhassa sayılar kuramı Öklid’in beşinci postülatı ve cebir alanında yoğunlaşmıştır. Elementler’e dair yaptığı bir yorum olan Risâle fî şerḥi mâ eşkele min muṣâderâti Kitâbi Öḳlîdis’te işlemler sırasında irrasyonel sayıların da rasyonel sayılar gibi kullanılabileceğini ilk defa o kanıtlamıştır. Bu eser ayrıca Öklid dışı geometrilerin kurulmasına öncülük etmiştir. Bu geometriler, Öklid’in paraleller postülatı adıyla da tanınan beşinci postülatının uzun süre iyi anlaşılamaması sebebiyle teorem sanılarak kanıtlanmaya çalışılması sonucu ortaya çıkmıştır. Bu çalışmalar içinde Doğu’da en esaslı olanlarından biri Ömer Hayyâm tarafından gerçekleştirilmiştir ve Batı’da ondan altı asır sonra konuyla ilk defa ilgilenen ve bundan dolayı Öklid dışı geometri araştırmalarının öncüsü sayılan İtalyan matematikçisi Giovanni Girolamo Saccheri’nin beşinci postülat üzerindeki incelemeleriyle dikkate değer bir benzerlik göstermektedir. Hayyâm, beşinci postülatı kanıtlamaya çalışırken daha sonra Saccheri’nin Euclides ab omni naevo vindicatus adlı eserinde aynı şekilde ele aldığı şöyle bir teorem geliştirmiştir: Birbirine eşit AC ve BD çizgilerini çektikten sonra AB ve CD’yi birleştirelim; ortaya şu üç durum çıkar:
C ve D açılarının ikisi de dik ise CD = AB’dir,
C ve D açılarının ikisi de geniş ise CD < AB’dir;
C ve D açılarının ikisi de dar ise CD > AB’dir.
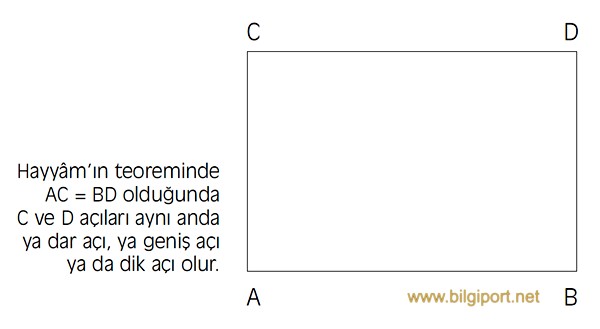
Ömer Hayyâm’a göre bu, beşinci postülatın kanıtlanmasıdır (Katz, s. 269-270). Dilgan da birinci durumun Öklid, ikinci durumun Riemann ve üçüncü durumun Lobatchewsky geometrilerine, diğer bir deyişle parabolik, eliptik ve hiperbolik geometrilere karşılık geldiğini söylemektedir (Şair Matematikci Ömer Hayyâm, s. 27-28).
Hayyâm’ın katkıda bulunduğu alanların en önemlisi cebirdir. Bu alanda üçüncü dereceden (kübik) denklemleri de kapsayan birçok cebirsel denklemi sınıflandırmış ve bunların çoğuna çözüm teklif etmiştir. Bu çözümlerin üçüncü dereceden denklemlere ilişkin olanları tam geometrik, diğerlerine ilişkin olanların çoğu kısmî geometriktir. En değerli cebir eserlerinden biri olan Risâle fi’l-berâhîn ʿalâ mesâʾili’l-cebr ve’l-muḳābele’de denklemlerin birden fazla köklerinin bulunabileceğini göstermiş ve bunları kök sayılarına göre sınıflandırmıştır. Bu arada üçüncü dereceden denklemleri terim sayılarına göre tasnif ettiği ve her grubun çözüm yöntemlerini belirlediği görülmektedir. Bu durumda üçüncü dereceden denklemler iki terimli, üç terimli ve dört terimli olarak üçe ayrılmaktadır ve iki terimli bir, üç terimli altı, dört terimli ise yedi tanedir:
x3 = d
x3 + cx = d
x3 + d = cx
x3 = cx + d
x3 + bx2 = d
x3 + d = bx2
x3 = bx2 +d
x3 + bx2 + cx = d
x3 + bx2 + d = cx
x3 + cx + d = bx2
x3 = bx2 + cx + d
x3 + bx2 = cx + d
x3 + cx = bx2 + d
x3 + d = bx2 + cx
Hayyâm bu denklemlerin aritmetik metotlarıyla çözülemeyeceğine inandığı için onları koni kesitleri (çember, parabol, hiperbol) yardımıyla geometrik biçimde çözmüş ve negatif kökleri daha önceki cebirciler gibi çözüm olarak kabul etmemiştir. Onun çözüm yöntemine örnek olarak şu üç terimli x3 + cx = d (bir küp kenarlar toplamı bir sayıya eşittir) üçüncü derece denklemini ele alalım:
x3 + cx = d denkleminin koni kesitleriyle çözümü
Ömer Hayyâm’ın Nîşâbur’daki türbesi
İbn Sînâ ekolüne mensup bir âlim-filozof olduğu kabul edilen Ömer Hayyâm cebir, geometri, astronomi, fizik ve tıpla ilgilenmiş, müzikle uğraşmış, ayrıca adını ölümsüzleştiren rubâîlerini kaleme almıştır. Ali b. Zeyd el-Beyhakī Hayyâm’ın hâfızasının fevkalâde kuvvetli olduğunu, dil, fıkıh, tarih ve kıraat sahalarında geniş mâlûmatı bulunduğunu, riyâziye, tıp ve diğer aklî ilimlerde eşsiz olduğunu söylerken Necmeddîn-i Dâye onun hakkında “bahtsız bir filozof, Allahsız ve maddeci” demektedir (İA, IX, 474). Ömer Hayyâm, Batı’da Doğu’nun en fazla hayranlık duyulan şairi ve en tanınmış âlimlerinden biridir. 1892’de Londra’da onun adına bir kulüp kurulmuş, 1970’te ayın üzerindeki bir kratere, 1980’de yeni bulunan bir kuyruklu yıldıza adı verilmiştir.
Ömer Hayyâm’ın Rubâʿiyyât’ının ilk iki sayfası (Süleymaniye Ktp., Erzincan, nr. 119)
Hayyâm’ın genelde matematiğin ve özelde analitik geometrinin gelişimi üzerindeki etkisi çok büyüktür; çalışmaları Şerefeddin et-Tûsî’ye (ö. 610/1213 [?]) kadar İslâm matematiğinde, üçüncü dereceden denklemlerin çözümünde geometrik yaklaşımı benimseyen Descartes’a (ö. 1650) kadar Batı matematiğinde aşılamamıştır. Onun matematiğe ilişkin araştırmaları ve bilhassa sayılar kuramı Öklid’in beşinci postülatı ve cebir alanında yoğunlaşmıştır. Elementler’e dair yaptığı bir yorum olan Risâle fî şerḥi mâ eşkele min muṣâderâti Kitâbi Öḳlîdis’te işlemler sırasında irrasyonel sayıların da rasyonel sayılar gibi kullanılabileceğini ilk defa o kanıtlamıştır. Bu eser ayrıca Öklid dışı geometrilerin kurulmasına öncülük etmiştir. Bu geometriler, Öklid’in paraleller postülatı adıyla da tanınan beşinci postülatının uzun süre iyi anlaşılamaması sebebiyle teorem sanılarak kanıtlanmaya çalışılması sonucu ortaya çıkmıştır. Bu çalışmalar içinde Doğu’da en esaslı olanlarından biri Ömer Hayyâm tarafından gerçekleştirilmiştir ve Batı’da ondan altı asır sonra konuyla ilk defa ilgilenen ve bundan dolayı Öklid dışı geometri araştırmalarının öncüsü sayılan İtalyan matematikçisi Giovanni Girolamo Saccheri’nin beşinci postülat üzerindeki incelemeleriyle dikkate değer bir benzerlik göstermektedir. Hayyâm, beşinci postülatı kanıtlamaya çalışırken daha sonra Saccheri’nin Euclides ab omni naevo vindicatus adlı eserinde aynı şekilde ele aldığı şöyle bir teorem geliştirmiştir: Birbirine eşit AC ve BD çizgilerini çektikten sonra AB ve CD’yi birleştirelim; ortaya şu üç durum çıkar:
C ve D açılarının ikisi de dik ise CD = AB’dir,
C ve D açılarının ikisi de geniş ise CD < AB’dir;
C ve D açılarının ikisi de dar ise CD > AB’dir.
Ömer Hayyâm’a göre bu, beşinci postülatın kanıtlanmasıdır (Katz, s. 269-270). Dilgan da birinci durumun Öklid, ikinci durumun Riemann ve üçüncü durumun Lobatchewsky geometrilerine, diğer bir deyişle parabolik, eliptik ve hiperbolik geometrilere karşılık geldiğini söylemektedir (Şair Matematikci Ömer Hayyâm, s. 27-28).
Hayyâm’ın katkıda bulunduğu alanların en önemlisi cebirdir. Bu alanda üçüncü dereceden (kübik) denklemleri de kapsayan birçok cebirsel denklemi sınıflandırmış ve bunların çoğuna çözüm teklif etmiştir. Bu çözümlerin üçüncü dereceden denklemlere ilişkin olanları tam geometrik, diğerlerine ilişkin olanların çoğu kısmî geometriktir. En değerli cebir eserlerinden biri olan Risâle fi’l-berâhîn ʿalâ mesâʾili’l-cebr ve’l-muḳābele’de denklemlerin birden fazla köklerinin bulunabileceğini göstermiş ve bunları kök sayılarına göre sınıflandırmıştır. Bu arada üçüncü dereceden denklemleri terim sayılarına göre tasnif ettiği ve her grubun çözüm yöntemlerini belirlediği görülmektedir. Bu durumda üçüncü dereceden denklemler iki terimli, üç terimli ve dört terimli olarak üçe ayrılmaktadır ve iki terimli bir, üç terimli altı, dört terimli ise yedi tanedir:
x3 = d
x3 + cx = d
x3 + d = cx
x3 = cx + d
x3 + bx2 = d
x3 + d = bx2
x3 = bx2 +d
x3 + bx2 + cx = d
x3 + bx2 + d = cx
x3 + cx + d = bx2
x3 = bx2 + cx + d
x3 + bx2 = cx + d
x3 + cx = bx2 + d
x3 + d = bx2 + cx
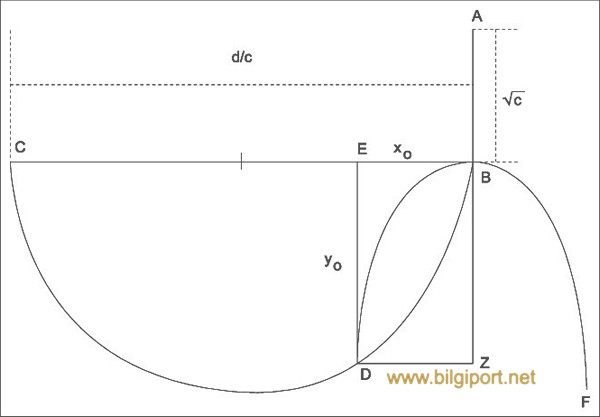
Hayyâm bu denklemlerin aritmetik metotlarıyla çözülemeyeceğine inandığı için onları koni kesitleri (çember, parabol, hiperbol) yardımıyla geometrik biçimde çözmüş ve negatif kökleri daha önceki cebirciler gibi çözüm olarak kabul etmemiştir. Onun çözüm yöntemine örnek olarak şu üç terimli x3 + cx = d (bir küp kenarlar toplamı bir sayıya eşittir) üçüncü derece denklemini ele alalım:
x3 + cx = d denkleminin koni kesitleriyle çözümü
Burada x bir küpün kenarını, c bir kareyi, d bir cismi gösterir. Hayyâm, önce çözümü geometrik çizimle yapmak için karenin bir kenarına eşit uzunlukta bir AB doğrusu çizer; yani =−−√AB=c olur. Sonra |2|=BCx|AB2|=d veya =BC=dcolacak şekilde AB doğrusuna dik BC doğrusunu çizer; AB’yi de Z yönünde uzatır. Böylece B tepe noktası BZ ekseninde ve AB parametresiyle bir parabol oluşturur. Modern ifadeye göre bu parabolün denklemi 2=−−√x2=cy’dir. Daha sonra BC üzerine bir yarım daire çizer. Bunun denklemi de (−2)2+2=(2)2(x−d2c)2+y2=(d2c)2 ya da (−)=2x(dc−x)=y2 ’dir. Daire ve parabol D noktasında kesişir ve bu noktanın x koordinatı olan BE doğru parçası denklemin çözümüdür. Bunun kanıtı ise şudur: Eğer BE=DZ=xo ve BZ=ED=yoise, D parabol üzerinde olduğundan önce 2=−−−√xo2=cyo yahut √=cxo=xoyo, sonra da 2=22=2(−)2=−=−cxo2=xo2yo2=yo2(dc−xo)2=yodc−xoxxoyo=xodc−xo elde edilir. O halde 3=−xo3=d−cxo’dır ve böylece xo da aranan çözümdür (Katz, s. 260-262; Gökdoğan, Bilim ve Ütopya, sy. 145 [2006], s. 12).
Üçüncü dereceden denklemleri sistemli bir şekilde çözdüğü için Hayyâm cebirde Hârizmî’nin gerçekleştirdiği gelişmenin ötesine geçmiştir. Ancak onun, üçüncü dereceden denklemlerin aritmetik çözümlerinin olamayacağına dair inancına karşı kendisinden sonra Şerefeddin et-Tûsî ile takipçileri bu tür denklemlerin aritmetik çözümlerinin bulunabileceğini göstermiştir. XVI. yüzyılda Batı’da bu tür denklemlerin aritmetik çözüm yöntemlerinin varlığı anlaşılmıştır. Hayyâm aynı zamanda cebirsel olguların geometrik olgular halinde ortaya çıktığını savunmuş, böylece Descartes’tan çok önce nümerik ve geometrik cebir arasındaki boşluğu kapatma yönünde önemli bir adım atmıştır. Onun bundan başka cebirde, n tam pozitif iken (a + b)n ifadesinin açınım formülünü Newton’dan önce kanunlaştırdığı söylenmekte, ayrıca aritmetik üçgen (Pascal veya Tartaglia üçgeni) adı verilen ve (a + b)n açınımındaki katsayılarla teşkil edilen şemanın da Hayyâm’a ait olduğu ileri sürülmektedir (Dilgan, Şair ve Matematikci Ömer Hayyâm, s. 6-7).
Astronomi alanına da büyük katkıları olan Ömer Hayyâm, İbnü’l-Esîr’in verdiği bilgiye göre 467 (1074-75) yılında Büyük Selçuklu Sultanı Melikşah tarafından İsfahan’a davet edilerek Ebû Hâtim İsfizârî, Meymûn b. Necîb el-Vâsıtî, Abdurrahman Hâris ve Muhammed Hâzin’den oluşan bir heyetin başkanlığına getirilmiş ve bir rasathâne kurup o yıllarda kullanılan Yezdicerd takvimini düzeltmekle görevlendirilmiştir. Ömer Hayyâm ile diğer bilim adamları yaptıkları çalışmalar sonucunda Yezdicerd takvimini düzeltmek yerine mevsimlere tam uyum gösterecek yeni bir takvim düzenlemenin daha doğru olacağına karar vermiş, böylece güneş yılı uzunluğu 365,2424 (modern ölçümlere göre gerçek uzunluk 365,2422) gün ve dolayısıyla hata payı 5000 yılda 1 gün olan Celâlî takvimi ortaya çıkmıştır. Heyet ayrıca Zîc-i Melikşâhî adlı bir zîc hazırlamış, kurulan rasathâne ise Melikşah’ın ölümüne (ö. 485/1092) kadar faaliyetini sürdürmüştür.
Hayyâm rubâîleriyle tanınmış bir şairdir. İmâdüddin el-İsfahânî Ḫarîdetü’l-ḳaṣr’ında onu Horasan şairleri arasında sayar ve örnek olarak Arapça bir rubâîsini verir. Rubâîlerin sayısının Rubâʿiyyât’ının istinsah tarihlerine göre günümüze yaklaştıkça arttığı görülmekte ve birçoğunun zamanla ona izâfe edilen başka şairlerin şiirleri olduğu anlaşılmaktadır. Kendi özgün üslûbunu yansıtan rubâîlerin sayısı 100 civarındadır. Rubâîlerinin Latince çevirileri XVIII. yüzyılda ortaya çıkmaya başlamıştır; T. Hyde’ın Veterum Persarum’unda onlardan biri yer alır. 1804’te F. Dombay’ın Viyana’da basılan Farsça gramerinde de bazı çeviriler bulunmaktadır. Hayyâm’ı bir şair olarak Batı’ya asıl tanıtan ve sevdiren ise Edward Fitzgerald’ın yaptığı İngilizce tercümelerdir.
Eserleri. 1. Rubâʿîyyât. Pek çok dile çevrilmiş, edisyon kritiği ilk defa J. B. Nicolas tarafından yapılmıştır (Les quatrains de Khèyam, Paris 1867; aş.bk.). 2. Risâle fî taḳsîmi rubʿi’d-dâʾire. Üçüncü dereceden denklemlerin çözüm yöntemlerine ve x3 + 200x = 20x2 + 2000 denkleminin çözümüne ilişkindir. Gulâm Hüseyin Musâhib tarafından Farsça çevirisiyle birlikte tıpkıbasımı yapılan eser (Ḥakîm ʿÖmer Ḫayyâm be-ʿUnvân-ı ʿÂlim-i Cebr, Tahran 1339 hş.) Rusça’ya (S. A. Krasnovoy – B. A. Rosenfeld, “Pervyy Algebraicheskiy Traktat”, Istoriko-Matematicheskiye issledovaniya, XV [Moscow 1963], s. 445-472), İngilizce’ye (Ali Rıza Amir Moèz, “A Paper of Omar Khayyam”, Scripta Mathematica, XXXVIII [1968], s. 205-208) ve Fransızca’ya (R. Rashed – A. Djebbar, L’oeuvre algébrique d’al-Khayyam, Aleppo 1981) çevrilmiştir. 3. Risâle fi’l-berâhîn ʿalâ mesâʾili’l-cebr ve’l-muḳābele. Denklemlerin sınıflandırılmasına ve her grubun çözüm yöntemlerine ilişkindir (Woepcke, L’algèbre d’Omar Alkayyâmî publiée, traduitée et accompagnée d’extraits de manuscrits inédits, Paris 1851; Daoud S. Kasir, The Algebra of Omar Khayyam, New York 1931; H. J. J. Winter – W. Arafat, “The Algebra of ‘Umar Khayyam”, JRASB, XVI [1950], s. 23-44). 4. Risâle fî şerḥi mâ eşkele min muṣâderâti Kitâbi Öḳlîdes. Öklid’in Elementler’i üzerine bir yorumdur (Takī İrânî, Risâle der Şerḥ-i Müşkilât-ı Muṣâderât-ı Kitâb-ı Öḳlîdis, Tahran 1314 hş.; Abdülhamîd Sabra [nşr.], Risâle fî şerḥi mâ eşkele min muṣâderâti Kitâb Öḳlîdis, İskenderiye 1381; Celâleddin Hümâî, Ḫayyâmînâme I, Tahran 1346 hş.; A. R. Amir Moèz, “’Omar al-Khayyami. Discussion of Difficulties of Euclid”, Scripta Mathematica, XXIV/4 [New York 1959], s. 275-303; Khalil Jaouiche, La théorie des parallès en pays d’Islam. Contribution à la préhistorie des géométries non-euclidiennes, Paris 1986). 5. Nevrûznâme. İsfahan’da Celâlî takvimi dahil kendi yönteminde hazırlanan takvimler üzerinedir (M. Mînovî [haz.], Nevrûznâme, Tahran 1312 hş.; Muhammed Abbâsî, Külliyyât-ı Âs̱âr-ı Pârsî-yi Ḥakîm ʿÖmer Ḫayyâm, Tahran 1338 hş.). 6. Zîc-i Melikşâhî. Hayyâm’ın kendi kurduğu gözlemevinde yapılan gözlem sonuçlarını içerir (V. S. Segalya – A. P. Yushevicha, “Traktaty”, Pervod Borisa A. Rosenfeld, Moskva 1962). 7. Mîzânü’l-ḥikem fî İhtiyâli maʿrifeti miḳdârey eẕ-ẕeheb ve’l-fiḍḍa fî cismin mürekkebin minhümâ. Metal alaşımlarındaki altın ve gümüş miktarının cebirsel yöntemlerle belirlenmesi hakkındadır. Abdurrahman el-Hâzinî tarafından tamamlanmıştır ve onun aynı adı taşıyan eserinin dördüncü kitabının beşinci bölümü içerisindedir. 8. Fi’l-ḳusṭâsi’l-müstaḳīm. Hayyâm’ın icat ettiği hidrostatik teraziyle ilgili olup Hâzinî’nin Mîzânü’l-ḥikem’inin yedinci kitabının sekizinci bölümünde geçer. 9. Silsile-i Tertîb (Risâle fî Külliyyâti’l-vücûd). Dört bölüm halindeki eserde birinci ve ikinci bölümler Fârâbîci ve İbn Sînâcı kozmolojinin temel öğeleri olan akıllar, nefisler ve unsurlarla madenler, bitkiler, hayvanlar ve insanlara, bunların aralarındaki ilişkilere dairdir. Üçüncü bölüm tümeller (külliyyât) ve kategoriler (makūlât), dördüncü bölüm hakikat konularını içerir (Abdülbaki Gölpınarlı, Hayyâm, Rubâiler ve Silsilat al-Tartîb ve İbn Sînâ’nın Tamcîd’i ve Tercümesi, İstanbul 1953). 10. el-Ḳavl ʿale’l-ecnâs elletî bi’l-erbaʿ. Eserde müzikte diatonik, kromatik ve harmonik olmayan tonlar ele alınır ve bu üç ton dışında 4/3 oranıyla gösterilen dördüncü bir ton daha verilir (Rahîm Rızâzâde Melik, s. 49-64). 11. el-Kevn ve’t-teklîf (a.g.e., s. 321-342). 12. Cevâb ʿan s̱elâs̱i mesâʾil: Żarûretü’t-teżâd fi’l-ʿâlem ve’l-cebr ve’l-beḳāʾ (a.g.e., s. 411-422). 13. eż-Żiyâʾ el-ʿaḳlî fî mevżûʿi’l-ʿilmi’l-küllî (a.g.e., s. 369-375). 14. Risâle fi’l-vücûd (a.g.e., s. 395-409). 15. Şerḥu’l-müşkil min Kitâbi’l-Mûsîḳā. 16. Levâzımü’l-emkine. Felsefî bir eserdir (eserlerinin bir listesiyle yazma nüshaları ve baskıları için bk. Youschkevitch – B. A. Rosenfeld, VIII, 331-333; Rosenfeld – İhsanoğlu, s. 168-170).
BİBLİYOGRAFYA
Ömer Hayyâm, Rubaîler (nşr. ve trc. Abdülbâki Gölpınarlı), İstanbul 1953; a.mlf., Resâʾilü’l-Ḫayyâm el-Cebriyye (nşr. Rüşdî Râşid – Ahmed Cebbâr), Halep 1981; Asaf Halet Çelebi, Ömer Hayyâm: Hayatı-Sanatı-Eserleri, İstanbul 1954; Hâmit Dilgan, Büyük Matematikci Ömer Hayyâm, İstanbul 1959; a.mlf., Şair Matematikci Ömer Hayyâm, İstanbul 1964; Sarton, Introduction, I, 759-761; A. Yuschkevitch – B. Rosenfeld, “Al-Khayyāmī (or Khayyām)”, DSB, VIII, 323-334; Ömer Akın – Melek Dosay, Beş Büyük Cebir Bilgini, Ankara 1994; Rahîm Rızâzâde Melik, Dânişnâme-i Ḫayyâmî, Tahran 1377 hş.; V. J. Katz, A History of Mathematics, An Introduction, New York 1998, s. 260-262, 269-270; I. Fernini, A Bibliography of Scholars in Medieval Islam: 150-1000 A.H. (750-1600 A.D.), Abu Dhabi 1998, s. 220-226; ‘Umar al-Khayyām, Text and Studies II (ed. Fuat Sezgin, Islamic Mathematics and Astronomy, XLVI içinde), Frankfurt 1998; İslâm Bilim ve Felsefesine Giriş (ed. Hakim Muhammed Said, trc. Remzi Demir), Ankara 1999, s. 54-56; Sevim Tekeli v.dğr., Bilim Tarihine Giriş, Ankara 2001, s. 215-218; Yavuz Unat, İlkçağlardan Günümüze Astronomi Tarihi, Ankara 2001, s. 100; a.mlf., “Ömer Hayyâm ve Melikşâh Gözlemevi”, Bilim ve Ütopya, sy. 145, İstanbul 2006, s. 13-14; Fâtıma Engûrânî – Zehra Engûrânî, Kitâbşinâsî-yi ʿÖmer Ḫayyâm: Bibliography of ʿOmar Khayyām, Tahran 1381 hş./2002; Melek Dosay Gökdoğan v.dğr., Bilim Tarihi Kılavuzu, Ankara 2001, s. 69, 291; Melek Dosay Gökdoğan, “Ömer Hayyâm’ın Cebiri”, Bilim ve Ütopya, sy. 145, İstanbul 2006, s. 11-12; Muhammed Ali-yi Furûgî v.dğr., Hayyâm: Hayatı, Felsefesi ve Gerçek Rubaîleri (trc. Hasan Çiftçi – Orhan Başaran), Erzurum 2002; B. A. Rosenfeld – Ekmeleddin İhsanoğlu, Mathematicians, Astronomers and Other Scholars of Islamic Civilization and Their Works (7th-19th c.), Istanbul 2003, s. 168-170; J. A. Boyle, “Omar Khayyam: Astronomer, Mathematician and Poet”, Bulletin of the John Rylands Library of Manchester, LII/1, Manchester 1969, s. 30-45; B. Vahabzadeh, “Al-Khayyām’s Conception of Ratio and Proportionality”, Arabic Sciences and Philosophy, VII, Cambridge 1997, s. 247-263; Remzi Demir, “Ömer Hayyâm’ın Felsefî Öğretisi Üzerine Bir Deneme”, Bilim ve Ütopya, sy. 145 (2006), s. 4-10; “Öklit’in 5. Postulası Üzerine El-Haytam’ın ‘Kanıt’ı ve Ömer Hayyam’ın Cevabı” (trc. Akgün Özsoy), a.e., sy. 145 (2006), s. 15-18; V. Minorsky, “Ömer Hayyâm”, İA, IX, 472-480; Ch.-H. de Fouchécour – B. A. Rosenfeld, “ʿUmar Khayyām”, EI2 (İng.), X, 827-834.
Bu bölüm ilk olarak 2007 senesinde İstanbul'da basılan TDV İslâm Ansiklopedisi’nin 34. cildinde, 66-68 numaralı sayfalarda yer almıştır.
Kaynak :
Üçüncü dereceden denklemleri sistemli bir şekilde çözdüğü için Hayyâm cebirde Hârizmî’nin gerçekleştirdiği gelişmenin ötesine geçmiştir. Ancak onun, üçüncü dereceden denklemlerin aritmetik çözümlerinin olamayacağına dair inancına karşı kendisinden sonra Şerefeddin et-Tûsî ile takipçileri bu tür denklemlerin aritmetik çözümlerinin bulunabileceğini göstermiştir. XVI. yüzyılda Batı’da bu tür denklemlerin aritmetik çözüm yöntemlerinin varlığı anlaşılmıştır. Hayyâm aynı zamanda cebirsel olguların geometrik olgular halinde ortaya çıktığını savunmuş, böylece Descartes’tan çok önce nümerik ve geometrik cebir arasındaki boşluğu kapatma yönünde önemli bir adım atmıştır. Onun bundan başka cebirde, n tam pozitif iken (a + b)n ifadesinin açınım formülünü Newton’dan önce kanunlaştırdığı söylenmekte, ayrıca aritmetik üçgen (Pascal veya Tartaglia üçgeni) adı verilen ve (a + b)n açınımındaki katsayılarla teşkil edilen şemanın da Hayyâm’a ait olduğu ileri sürülmektedir (Dilgan, Şair ve Matematikci Ömer Hayyâm, s. 6-7).
Astronomi alanına da büyük katkıları olan Ömer Hayyâm, İbnü’l-Esîr’in verdiği bilgiye göre 467 (1074-75) yılında Büyük Selçuklu Sultanı Melikşah tarafından İsfahan’a davet edilerek Ebû Hâtim İsfizârî, Meymûn b. Necîb el-Vâsıtî, Abdurrahman Hâris ve Muhammed Hâzin’den oluşan bir heyetin başkanlığına getirilmiş ve bir rasathâne kurup o yıllarda kullanılan Yezdicerd takvimini düzeltmekle görevlendirilmiştir. Ömer Hayyâm ile diğer bilim adamları yaptıkları çalışmalar sonucunda Yezdicerd takvimini düzeltmek yerine mevsimlere tam uyum gösterecek yeni bir takvim düzenlemenin daha doğru olacağına karar vermiş, böylece güneş yılı uzunluğu 365,2424 (modern ölçümlere göre gerçek uzunluk 365,2422) gün ve dolayısıyla hata payı 5000 yılda 1 gün olan Celâlî takvimi ortaya çıkmıştır. Heyet ayrıca Zîc-i Melikşâhî adlı bir zîc hazırlamış, kurulan rasathâne ise Melikşah’ın ölümüne (ö. 485/1092) kadar faaliyetini sürdürmüştür.
Hayyâm rubâîleriyle tanınmış bir şairdir. İmâdüddin el-İsfahânî Ḫarîdetü’l-ḳaṣr’ında onu Horasan şairleri arasında sayar ve örnek olarak Arapça bir rubâîsini verir. Rubâîlerin sayısının Rubâʿiyyât’ının istinsah tarihlerine göre günümüze yaklaştıkça arttığı görülmekte ve birçoğunun zamanla ona izâfe edilen başka şairlerin şiirleri olduğu anlaşılmaktadır. Kendi özgün üslûbunu yansıtan rubâîlerin sayısı 100 civarındadır. Rubâîlerinin Latince çevirileri XVIII. yüzyılda ortaya çıkmaya başlamıştır; T. Hyde’ın Veterum Persarum’unda onlardan biri yer alır. 1804’te F. Dombay’ın Viyana’da basılan Farsça gramerinde de bazı çeviriler bulunmaktadır. Hayyâm’ı bir şair olarak Batı’ya asıl tanıtan ve sevdiren ise Edward Fitzgerald’ın yaptığı İngilizce tercümelerdir.
Eserleri. 1. Rubâʿîyyât. Pek çok dile çevrilmiş, edisyon kritiği ilk defa J. B. Nicolas tarafından yapılmıştır (Les quatrains de Khèyam, Paris 1867; aş.bk.). 2. Risâle fî taḳsîmi rubʿi’d-dâʾire. Üçüncü dereceden denklemlerin çözüm yöntemlerine ve x3 + 200x = 20x2 + 2000 denkleminin çözümüne ilişkindir. Gulâm Hüseyin Musâhib tarafından Farsça çevirisiyle birlikte tıpkıbasımı yapılan eser (Ḥakîm ʿÖmer Ḫayyâm be-ʿUnvân-ı ʿÂlim-i Cebr, Tahran 1339 hş.) Rusça’ya (S. A. Krasnovoy – B. A. Rosenfeld, “Pervyy Algebraicheskiy Traktat”, Istoriko-Matematicheskiye issledovaniya, XV [Moscow 1963], s. 445-472), İngilizce’ye (Ali Rıza Amir Moèz, “A Paper of Omar Khayyam”, Scripta Mathematica, XXXVIII [1968], s. 205-208) ve Fransızca’ya (R. Rashed – A. Djebbar, L’oeuvre algébrique d’al-Khayyam, Aleppo 1981) çevrilmiştir. 3. Risâle fi’l-berâhîn ʿalâ mesâʾili’l-cebr ve’l-muḳābele. Denklemlerin sınıflandırılmasına ve her grubun çözüm yöntemlerine ilişkindir (Woepcke, L’algèbre d’Omar Alkayyâmî publiée, traduitée et accompagnée d’extraits de manuscrits inédits, Paris 1851; Daoud S. Kasir, The Algebra of Omar Khayyam, New York 1931; H. J. J. Winter – W. Arafat, “The Algebra of ‘Umar Khayyam”, JRASB, XVI [1950], s. 23-44). 4. Risâle fî şerḥi mâ eşkele min muṣâderâti Kitâbi Öḳlîdes. Öklid’in Elementler’i üzerine bir yorumdur (Takī İrânî, Risâle der Şerḥ-i Müşkilât-ı Muṣâderât-ı Kitâb-ı Öḳlîdis, Tahran 1314 hş.; Abdülhamîd Sabra [nşr.], Risâle fî şerḥi mâ eşkele min muṣâderâti Kitâb Öḳlîdis, İskenderiye 1381; Celâleddin Hümâî, Ḫayyâmînâme I, Tahran 1346 hş.; A. R. Amir Moèz, “’Omar al-Khayyami. Discussion of Difficulties of Euclid”, Scripta Mathematica, XXIV/4 [New York 1959], s. 275-303; Khalil Jaouiche, La théorie des parallès en pays d’Islam. Contribution à la préhistorie des géométries non-euclidiennes, Paris 1986). 5. Nevrûznâme. İsfahan’da Celâlî takvimi dahil kendi yönteminde hazırlanan takvimler üzerinedir (M. Mînovî [haz.], Nevrûznâme, Tahran 1312 hş.; Muhammed Abbâsî, Külliyyât-ı Âs̱âr-ı Pârsî-yi Ḥakîm ʿÖmer Ḫayyâm, Tahran 1338 hş.). 6. Zîc-i Melikşâhî. Hayyâm’ın kendi kurduğu gözlemevinde yapılan gözlem sonuçlarını içerir (V. S. Segalya – A. P. Yushevicha, “Traktaty”, Pervod Borisa A. Rosenfeld, Moskva 1962). 7. Mîzânü’l-ḥikem fî İhtiyâli maʿrifeti miḳdârey eẕ-ẕeheb ve’l-fiḍḍa fî cismin mürekkebin minhümâ. Metal alaşımlarındaki altın ve gümüş miktarının cebirsel yöntemlerle belirlenmesi hakkındadır. Abdurrahman el-Hâzinî tarafından tamamlanmıştır ve onun aynı adı taşıyan eserinin dördüncü kitabının beşinci bölümü içerisindedir. 8. Fi’l-ḳusṭâsi’l-müstaḳīm. Hayyâm’ın icat ettiği hidrostatik teraziyle ilgili olup Hâzinî’nin Mîzânü’l-ḥikem’inin yedinci kitabının sekizinci bölümünde geçer. 9. Silsile-i Tertîb (Risâle fî Külliyyâti’l-vücûd). Dört bölüm halindeki eserde birinci ve ikinci bölümler Fârâbîci ve İbn Sînâcı kozmolojinin temel öğeleri olan akıllar, nefisler ve unsurlarla madenler, bitkiler, hayvanlar ve insanlara, bunların aralarındaki ilişkilere dairdir. Üçüncü bölüm tümeller (külliyyât) ve kategoriler (makūlât), dördüncü bölüm hakikat konularını içerir (Abdülbaki Gölpınarlı, Hayyâm, Rubâiler ve Silsilat al-Tartîb ve İbn Sînâ’nın Tamcîd’i ve Tercümesi, İstanbul 1953). 10. el-Ḳavl ʿale’l-ecnâs elletî bi’l-erbaʿ. Eserde müzikte diatonik, kromatik ve harmonik olmayan tonlar ele alınır ve bu üç ton dışında 4/3 oranıyla gösterilen dördüncü bir ton daha verilir (Rahîm Rızâzâde Melik, s. 49-64). 11. el-Kevn ve’t-teklîf (a.g.e., s. 321-342). 12. Cevâb ʿan s̱elâs̱i mesâʾil: Żarûretü’t-teżâd fi’l-ʿâlem ve’l-cebr ve’l-beḳāʾ (a.g.e., s. 411-422). 13. eż-Żiyâʾ el-ʿaḳlî fî mevżûʿi’l-ʿilmi’l-küllî (a.g.e., s. 369-375). 14. Risâle fi’l-vücûd (a.g.e., s. 395-409). 15. Şerḥu’l-müşkil min Kitâbi’l-Mûsîḳā. 16. Levâzımü’l-emkine. Felsefî bir eserdir (eserlerinin bir listesiyle yazma nüshaları ve baskıları için bk. Youschkevitch – B. A. Rosenfeld, VIII, 331-333; Rosenfeld – İhsanoğlu, s. 168-170).
BİBLİYOGRAFYA
Ömer Hayyâm, Rubaîler (nşr. ve trc. Abdülbâki Gölpınarlı), İstanbul 1953; a.mlf., Resâʾilü’l-Ḫayyâm el-Cebriyye (nşr. Rüşdî Râşid – Ahmed Cebbâr), Halep 1981; Asaf Halet Çelebi, Ömer Hayyâm: Hayatı-Sanatı-Eserleri, İstanbul 1954; Hâmit Dilgan, Büyük Matematikci Ömer Hayyâm, İstanbul 1959; a.mlf., Şair Matematikci Ömer Hayyâm, İstanbul 1964; Sarton, Introduction, I, 759-761; A. Yuschkevitch – B. Rosenfeld, “Al-Khayyāmī (or Khayyām)”, DSB, VIII, 323-334; Ömer Akın – Melek Dosay, Beş Büyük Cebir Bilgini, Ankara 1994; Rahîm Rızâzâde Melik, Dânişnâme-i Ḫayyâmî, Tahran 1377 hş.; V. J. Katz, A History of Mathematics, An Introduction, New York 1998, s. 260-262, 269-270; I. Fernini, A Bibliography of Scholars in Medieval Islam: 150-1000 A.H. (750-1600 A.D.), Abu Dhabi 1998, s. 220-226; ‘Umar al-Khayyām, Text and Studies II (ed. Fuat Sezgin, Islamic Mathematics and Astronomy, XLVI içinde), Frankfurt 1998; İslâm Bilim ve Felsefesine Giriş (ed. Hakim Muhammed Said, trc. Remzi Demir), Ankara 1999, s. 54-56; Sevim Tekeli v.dğr., Bilim Tarihine Giriş, Ankara 2001, s. 215-218; Yavuz Unat, İlkçağlardan Günümüze Astronomi Tarihi, Ankara 2001, s. 100; a.mlf., “Ömer Hayyâm ve Melikşâh Gözlemevi”, Bilim ve Ütopya, sy. 145, İstanbul 2006, s. 13-14; Fâtıma Engûrânî – Zehra Engûrânî, Kitâbşinâsî-yi ʿÖmer Ḫayyâm: Bibliography of ʿOmar Khayyām, Tahran 1381 hş./2002; Melek Dosay Gökdoğan v.dğr., Bilim Tarihi Kılavuzu, Ankara 2001, s. 69, 291; Melek Dosay Gökdoğan, “Ömer Hayyâm’ın Cebiri”, Bilim ve Ütopya, sy. 145, İstanbul 2006, s. 11-12; Muhammed Ali-yi Furûgî v.dğr., Hayyâm: Hayatı, Felsefesi ve Gerçek Rubaîleri (trc. Hasan Çiftçi – Orhan Başaran), Erzurum 2002; B. A. Rosenfeld – Ekmeleddin İhsanoğlu, Mathematicians, Astronomers and Other Scholars of Islamic Civilization and Their Works (7th-19th c.), Istanbul 2003, s. 168-170; J. A. Boyle, “Omar Khayyam: Astronomer, Mathematician and Poet”, Bulletin of the John Rylands Library of Manchester, LII/1, Manchester 1969, s. 30-45; B. Vahabzadeh, “Al-Khayyām’s Conception of Ratio and Proportionality”, Arabic Sciences and Philosophy, VII, Cambridge 1997, s. 247-263; Remzi Demir, “Ömer Hayyâm’ın Felsefî Öğretisi Üzerine Bir Deneme”, Bilim ve Ütopya, sy. 145 (2006), s. 4-10; “Öklit’in 5. Postulası Üzerine El-Haytam’ın ‘Kanıt’ı ve Ömer Hayyam’ın Cevabı” (trc. Akgün Özsoy), a.e., sy. 145 (2006), s. 15-18; V. Minorsky, “Ömer Hayyâm”, İA, IX, 472-480; Ch.-H. de Fouchécour – B. A. Rosenfeld, “ʿUmar Khayyām”, EI2 (İng.), X, 827-834.
Bu bölüm ilk olarak 2007 senesinde İstanbul'da basılan TDV İslâm Ansiklopedisi’nin 34. cildinde, 66-68 numaralı sayfalarda yer almıştır.
Linkleri görmek için
Giriş yap veya üye ol.
Kaynak :
Linkleri görmek için
Giriş yap veya üye ol.